World: How time really works

Time is like the graph of y = 1/x.

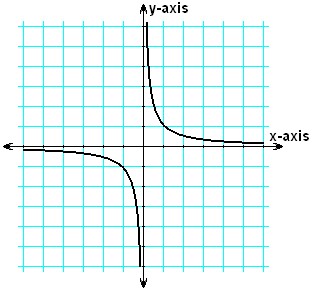
This is an attempt to explain the big bang. It's a simple model that can help understand what happens closer to the event itself.

I will call the graph 'experience'. We experience time and... something else. Let's call that something ujnf (pronounced 'ujnif'). Time=x; ujnf=y.

Of course, experience only moves in one direction (as far we are aware). We're in the positive quadrant, a fair bit down the time track where x is a fairly large number and the line appears to us as quite flat. We really only know experience as time, with no discernable aspect in the y, or ujnf, dimension.

The origin, where x=0 and y=0, is the big bang - ie the beginning of the universe. As you can see, we can never actually get there. As we look backwards along the experience line, the secondary dimension, ujnf, actually moves a little bit, and as we get closer to the big bang, the time dimension slows right down. Eventually experience is moving nearly entirely in the ujnf dimension.

With this model, time slows down moving closer to the big bang, but you never actually get there. I believe that squares with some other views on that end of the universe - and it answers the question: what happened before the big bang? Answer: you can never actually get there (per below, it would be like trying to cross to a different universe). Close to the event, time slows down - but experience moving in a different direction. Not that this could be experienced, just conceptualised.

This means:

a) if we could travel backwards in time - or rather, experience - we'd never actually get to the big bang, because although experience would continue as ujnf, the time component would slow down until it effectively stops.

b) the big bang is a singularity, and like all singularities (black holes in particular) we can never actually experience it. (In black holes, time also slows down, but gravity would rip us to pieces, probably before we started experiencing ujnf.)

Questions:

1) What is ujnf?

2) Are we really too far down the track to experience ujnf at all?

3) Would we have the senses to feel ujnf?

4) What is that negative part of the graph - negative time and negative ujnf? Obviously it's before the start of the universe, but how do we conceptualise it?

5) In the conceptual model, what does it mean if we move the experience line closer to the origin - eg y=1/x squared?

6) As I said, it's only a simple model. For example, why should there be only two dimensions?

There are several ways in which this can tie in with physicist Leonard Susskind's conceptualisation of multiple universes. Most of those methods - except 5) & 6) above - would involve crossovers from one universe to another. I doubt that would be possible, so let's just stick to crossing to another universe via (impossible) movement in the direction of y=x. But his is more in the realm of science fiction, as far as we know today.

I came up with this model some years back. Are there any theoretical developments that either mimic or negate this? Your comments please.

(I reserve the right to refine this discussion as time goes by. If not ujnf.)

* Thanks to Wikibooks for the chart.