Tech: The beauty in Mathematics

Mathematics certainly is beautiful. But I do understand that it’s a struggle for a lot of people. It’s hard to communicate that beauty to someone for whom maths is simply a source of frustration, so I don’t expect universal agreement on this.

I stumbled across a Wikipedia article called Mathematical Beauty. Rather an unusual encyclopaedia entry, but in many ways ideal: to have a subject presented from an enthusiast’s viewpoint should be the starting point for any subject. Read the quotes at the beginning of the article: good perspective from some famous aficionadoes.

I studied pure mathematics as an undergraduate major, and it was greatly enjoyable. It’s a puzzle enthusiast’s joy for the solution, or the reader’s joy in elegant prose, a well-constructed plot, or a moving journey. Except that in this case, you’re seeing beauty in a ruthless, immutable truth.

The discussion of various types of beauty in maths is something that strikes a chord with me. Beauty in method is what mathematicians typically refer to as elegance; this is my most common experience of beauty. But I particularly appreciate a line of thought that draws in two seemingly unrelated strands of thought – beauty in results. Calculus is good for this. And the recently-created proof of Fermat’s Last (unsolved) Theorem – which took several years of the solver’s life – is a good illustration of the value – and capability, and necessity – of drawing in different branches of thought.


But I particularly love Euler’s Identity – which is about the most beautiful formula I’ve ever seen, for its elegance, simplicity, and deepness:

- three of the most basic constants for the price of one, all tied back to the identity.

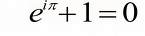
A reminder: e is the base of the natural logarithm (ln), i is an imaginary unit on the complex number plane (the square root of -1), and pi is, well, pi (ratio of a circle's circumference to diameter). Its journey describles the semi-circumference of a unit circle from 1 to -1.

An appreciation of mathematics is the root of all science.

World: Bees in the bonnet 2: Increasing terrorism

We all heard about the US report finding there has been an increase in terrorism in recent years. The first news I heard about that suggested the Iraq war/occupation had contributed to this, but I didn't read that into the Washington Post report.

However, I would concur. The US has painted itself into a bad corner. There's no doubt Saddam Hussein was viciously evil, and his regime deserved to die. And there's no doubt that release brought on a lot of sectarian violence, much as the death of Tito did for Yugoslavia.

But it's not hard to say that the US buried their goodwill in unethical behaviour. It's hard to be saints, but Abu Ghraib was allowed to happen, via a culture that was directed by the ethics at the top. Similarly the knowingly false grounds for entering Iraq - WMD - which had only slim pretense of being sanctioned by the UN.
And, most jarring of all, continued financial support for Israel, without pushing them to settle with their neighbours.

Constructive ethics is harder. It's slower, and sometimes more costly upfront. But... a quote from Bill Clinton:

"Since we can't kill, jail or occupy all of our enemies ... we also have to spend some time and money making more and more partners and fewer enemies," he said. "It is so much cheaper to alleviate poverty, put kids in school, fight disease ... in a poor country than it is to fight a war."

Well, that's how you win a war. That's how you nation-build.

Of course, this is easy for anyone to say. The US political beast is a hard one to manage; it needs someone with vision. And ethics.

Tech: Don't waste your time on a Data warehouse!

Dratz did an interesting post on data warehousing.

In effect: why bother?

In concept, a data warehouse is laudible: one place where you can store all the organisation's data, integrated across business units...

But why? Do you have a business case for it? A good reason you can't extract the intelligence you want from the existing databases?

Well maybe you can't. But maybe you can. Dratz pointed out that the "if you build it they will come" philosophy is the ruin of many a technologist. It just doesn't necessarily happen.

At my workplace, there's a data warehouse. But does it contain feeds from all the company's repositories? Noooo. In fact, much as you'd like to think the organisation is all one big happy family, there remain concepts of ownership. Competition, even.

Break down the information silos? Look at the business silos first. Work on the business issues, the internal politics. And tell me integration is axiomatic.


All I'm saying is, think more carefully about what you're doing. If there's a green light, start small. Don't try to bring on board business units that aren't yet interested - or even jealously guard their IP. Datawarehouse by all means, but only as and when there are specific business returns.

World: Putting bees in the bonnet 1: Chavez and Chomsky

So much to blog about, so little time... sigh.

Now what shall we do today... well, an easy one is this picture:


Unless you've been under a rock, you'd recognise this as Hugo Chavez, Venezuela's president, addressing the UN General Assembly, and waving a copy of Noam Chomsky's book Hegemony or Survival: America's Quest for Global Domination. Two provocative people for the price of one.

Now watch the book go! On Amazon, from 160,772nd best seller to 22nd overnight... to 7th... to 3rd...

A week later, it's back at number 40, which is still no mean feat by any stretch.


Now, Chomsky, I believed, was more an anarchist, and Chavez a left winger. And only occasionally do the twain happen to meet. However, I'm willing to stand corrected on the basis of Chomsky's Wikipedia entry, which says he considers himself a libertarian socialist with anarchist sympathies. And he's a wobbly - I didn't even realise they were still around.

And apparently, Time magazine this year rated Chavez as one of the world's 100 most influential people. (Gee, I must have been living under a rock!)

Ahh, I'm rambing. Still, never thought I'd see either of the blokes capable of causing such a stir, in this brave new century.

Tech: How hard is it to avoid leaving traces?

Data is so persistent - and pervasive - that it's hard to ensure a secret is kept, once it's online.

By that, I mean that traces always remain, somewhere. For example, if you send an email to someone, you may live to regret it. But you can't expunge it. There's the copy on your computer, one on the recipient's computer, and one on each of the email servers of the ISPs that service each end. And despite what ISPs say about the difficulty of retrieving an accidentally-deleted email, can you be sure that your message is not archived somewhere? - indefinitely?

Enter Vapourware with a whole new meaning.

This report discusses a new product called VaporStream. One person types in a message to the application, it is stored temporarily on a server somewhere - securely - where someone else can click to read it once - but not copy it. After reading, the message is deleted from the server permanently.

Of course, this is not for everyone. As the article points out, much of a business' electronic activities have a legislative requirement to be stored. But there is also an amount of message transactions that are actually a pain to retain, and difficult to completely remove.

And, of course, people have secrets, that they don't want persisting in stored messages.


However, I can see a simple flaw in this. You cannot guarantee the recipient hasn't done this: capture a screenshot of the message, via the ctl-print scrn buttons.

But if you trust the recipient, this may be your best punt at preventing your secret pervading.

Climate Change: Remember those responsible!

A recent article in the New Scientist stuck in my memory. More correctly, the opening thoughts did, and they can be paraphrased thus:

What I love about science is that it is ruthless. It doesn’t matter what you believe – or say you believe – it is the way it is.


Pretending otherwise is like legislating that pi = 3: it will make calculations easier, but all kinds of engineering problems will arise. Bridges will fall, and buildings will crumble.

Now hold that thought for a moment.


It has occurred to me that some people seem to be back-peddling on climate change. The latest is Australia’s PM John Howard, who said words to the effect that terrorism is more important than climate change. That’s one up from his past denial that climate change has any importance at all. But maybe on a par with his “thought” that economic growth is more important than climate change, and that it’s a matter of one or the other.


So, take a snapshot of their positions. People like that in pivotal positions are the ones responsible for dithering on the issue. They are the ones to hold accountable when, at some point in the future, everyone readily acknowledges the issue, but they acted too late, and the seas have already risen a metre.

Why has the sea risen? As we’ve seen before (again, from New Scientist), the ice in Greenland alone will raise the sea level several metres. And Greenland’s ice cap is a) above sea level, and b) melting right now.

The science is there already, so there’s no excuse. For ideological and other reasons, those people are ignoring the science. Maybe they hope they’ll be dead before the effects are felt. But if they’re not, hold them culpable. Tell them what world they have created for their grandchildren.


Those of us not in positions of influence can still do something. We can lead the way in our own actions. Of itself, one person’s actions will not do a lot. But many in the vanguard can make a critical mass that will impel action in those in power.

A reminder of the simplest things you can do:
- use public transport more; use the car less;
- put your superannuation money into ethical funds
- take your electricity from 100% renewable sources
- use your vote to focus the issue
- spread the word about your concern.

Tech: Ethnography of web sites

What does ethnography have to do with web sites?

What is ethnography?

Well, I had to look it up. It's field-study anthropology. In effect, studying cultures in the field, over a period of time - years, maybe! - and writing it up, perhaps in a comparative sense, perhaps on and of the culture by itself.


The second talk at a recent Web Directions seminar (previous posted on Remember The Milk) was from a guy who was hired to investigate the use of a sports web site, and how to improve its attraction to sports fans.

The researcher was ideal: like me, he had very little interest in sports. That, I feel, made the study less skewed, more... anthropological, in fact.

It was apparently a worthwhile exercise. He identified what drove sports fans, what they wanted to read about, how, when and why.

He had a couple of terms that demonstrated his success in coming to grips with the subject matter: BARGs and CORFs. That is, depending on whether your team wins, you:

Bask in Reflected Glory; or
Cut Off Reflected Failure.

And whichever side you supported, you want to see reasons for the result in what you read.

Of course, I tested it out on someone whose team was losing. It was close to the finals, and he was CORFing so much he baulked whenever the subject was mentioned.

And the web site that this bloke helped improve so much? Well, I'm not a commercial forum, but if you're a sports fan, you can ask me... and then you can tell me how successful you feel it is.

World: Why low interest rates DON'T help house buyers

An interesting article by Ross Gittens in the Herald points out that the reason house prices have gone up so much in Sydney is simply that interest rates have gone down.

In effect, people pay what they can afford to pay for scarce commodities, and houses in the east of Sydney (to a lesser extent in the west) are scarce commodities.

When interest rates went down from a high of 17%, it simply meant that the same people were chasing the same houses, but could afford to bid more.

Of course, the big winners are the banks. And the politicians who claim (falsely) that they made the interest rates go down, and that it's a good thing. From the point of view of business, it is a good thing (as long as inflation doesn't soar).

But from the point of view of house owners, the banks end up taking whatever people can afford to pay, regardless the interest rate.

Tech: business/technical engagement always problematic

I may have said this before, but I’m not above reiterating it: there is too often a disconnect between business requirements and technical delivery.

In an ideal world, the business requirements are specified, and the technical team delivers.

In a real world, the technical team delivers something, the business team finds it’s not quite what they wanted because of the way the technical environment structures the business information, and there are several more iterations to go through.


A few weeks ago, I pushed to have access to the technical environment, although I was going to be specifying business requirements, as oppposed to delivering on them. It was a struggle to get the technical access, but they eventually acceded.
Benefits:

a) the technical environment frees me from the shackles of the technical team’s limitations, including resource availability;
b) without navigating the business information within the technical environment, I couldn’t get a clear picture of what was achievable, and broadly how to achieve it.

Now I know better what to tell the technical guys, so they don't get it wrong. And I push onto them the technical issues that I can see need resolving.

World: Sydney Opera House (3): Another discarded design

This one is said to be a "concept" rather than a definite proposal, put forward by the then-conductor of the Sydney Symphony, Eugene Gossens, for the 1956 design competition for Sydney Opera House.

Film: The subtlety of fable in Lady In The Water (US, 2006)

I can only assume all the reviewers I’ve read have ignored the underlying fable in Lady In The Water because the superficial story was too twee or contrived for them.

However, it could be said that most Hollywood storytelling is twee and/or contrived, so I remain at a loss.

I have a lot of respect for M Night Shyamalan’s skill and imagination as a storyteller. The breadth of his vision compares favourably with that of the better science fiction writers. His milieu tends to be more the supernatural, but like science fiction, it can be used to free the writer to better tell the story.

On the surface, this is a fable of a water nymph, comprising a very specific mythology which Shyamalan completely invented.

The overlooked fable, however, is more about the role an individual can play in a wider narrative, a greater good. However slight a single person’s part is, they can achieve wonders when united with the small parts of others.

That person can make mistakes, misunderstand their role – and may not even understand the greater picture. But if the good will is there, their achievement can be profound nevertheless.

There may also be in this story a smaller fable about the power of trauma to forge a humility in someone, that can aid in the greater good.


This is fable, of course, because good doesn’t axiomatically come out of good; the good can die in vain as the selfish prosper. But is that necessarily so? Who knows what ripples fan out from our actions? How long away before the small part we play manifests in some greater good?

A fable of hope, that can be part of reality.

Tech: Unified theory is all very well, but

6.36pm
In quantum mechanics, a particle is in several places at once, yet only exists in one of those places when you look at it.

Obviously, it exists across all space-times in that point. That is why, whenever you view a particle it only appears at one point, because at all other of those points, of that inhabited space, it is in all other space-times in the dimensional universe.

This may or may not speak to concepts of travel or alternative universes. I wouldn't stick my head out.

Tech: Choose: tv, phone or computer

What's more important to you, out of your tv, computer, or mobile phone?

Industry analysts Forrester posed this in a poll, and found tv came tops.

However, looking more closely, tv was bottom in the 18 - 26 age group. A portent for the future: Further evidence that competition for people's attention is fierce, and that tv no longer plays the central role in lives of the young that it once did.

Interestingly, that age group rated computers above phones. Further, computers were tops with more affluent people. It's likely fewer of the less affluent have computers - again, evidence they spend money on tv first. (Well, it's also cheaper.)

Also suggestive that the digital divide is entrenching itself. If you consider computers (and thus internet) absolutely key to one's access to information and knowledge, then this is certainly an issue for public policy makers.

World: Children exposed to too much, too early

A news report details concerns from childhood experts in the UK that children are exposed far too early to adult issues. Yes, this has been raised before, but as they said, we are in an unprecedented era of rapid technological and cultural change. They decry the loss of “real food, real play” – which is undeniably an aspect of most recent times.

I would add to that exposure to issues of sex, violence, and world issues that are too complex to absorb with equanimity.

This is a serious issue. I see in my kids a genuineness, an innocence, that is lost to adults. It’s a magical time, a beauty that is yet easily witnessed by adults. This is a loss to all.

My only thoughts are to feed the children slow food, get them active, and keep them away from any kind of screen as much as possible.

Tech: Who’s Huawei? The tech growth path

Several announcements in recent times indicated that Huawei Technologies is making marked inroads into the Australian technology market.

Huawei not a household name. Yet. But they seem to be selling very well around the world, in the pre-consumer sphere.

They’re a Chinese telecommunications hardware manufacturer. The signs are that they go in cheap – possibly ultra-cheap – with a product range that is not quite as reliable as their better known competitors. If their reliability is at issue, then for major telcos to take the plunge they must be seeing severe cost savings.

So if your telecoms infrastructure is hiccupping, the reason may be that service quality is the end cost of driving prices down.

Of course, this scenario is familiar. It’s the path taken by Japanese manufacturers in the 50s and 60s. Sell cheap, build up a brand name, and slowly ramp up the technology on the back of success.

And look what that did for Japan.

World: Credit to a true conservationist

Like a number of Australians, I was rather surprised by the sudden global interest in Steve Irwin. I’ll stick my neck out and say he was possibly more popular overseas than in Australia.

I read that this was the biggest news item ever to spread on the internet (partly because the internet population is now much bigger than it was a scant few years ago). Even Securitymonkey blogged off-topic – something I’ve never seen before.


Not that I knew too much about Irwin, but personally, I didn’t care for yet another cartoonish portrayal of Australia, like Skippy or Crocodile Dundee.

However, I was also surprised to find out he was a genuine conservationist, who popularised such issues, disdained a wealthy lifestyle, and ploughed most of his money back into conservation, in one form or another. I’m not prone to eulogising someone just because they’re dead, but I’m certainly happy to praise someone who works for the better good.

On a personal level, it’s rather close to the bone that he was born just a month before me, and also had two young kids. Sobering.

World: word of the day

dace
–noun, plural (especially collectively) dace, (especially referring to two or more kinds or species) dac‧es.
1. a small, freshwater cyprinoid fish, Leuciscus leuciscus, of Europe, having a stout, fusiform body.

cadi
\Ca"di\, n. [Turk.] An inferior magistrate or judge among the Mohammedans, usually the judge of a town or village.

Source: dictionary.com

Just thought you’d like to know a couple of words from the target puzzle a couple of days ago. Obviously, they’re words you’d want to get on top of, practice using them – in particular, you could try using both in one sentence, as in:
“the cadi sat back and burped his pleasure [as is the custom] after the fine meal of dace.” This begs the question how a village magistrate in Turkey would be eating european fish – and of course, whether that fish is edible. But therein lies the makings of a story in itself.

Of course, you’d have to think up your own sentence…

Tech: Remember the milk - and Ajax

Remember the milk is a website originating in Australia, with some novel features for scheduling reminders. It must be good, because their marketing consisted entirely of telling a few friends, and usage is now in the millions.

I was fortunate enough to attend a presentation on it last week, given by its instigator Emily Boyd, under the auspices of an evening put together by the webdirections people.

The special features are enabled by Ajax, a set of technologies that enables web pages to be refreshed at the client end without need for a refresh from the server (ie Asynchronously - it also makes use of JavaScript And XML technology).

This allows the application to read and interpret data entry as it's typed. Further, entering a schedule date is made easy with intuitive language interpretation, eg "next wednesday" or "every fortnight from the 21st". All this is apparently painful to program, but yields a very user-friendly interface: "enter as you think".

Another little quirk is: instead of an annoying dialogue box: "do you really want to delete?", it yields an "undelete" function. Again very friendly. Microsoft will probably quietly introduce improvements like this...

World: Hippies get real

Whatever happened to hippies?

Judging by this article (first published in the Sydney Morning Herald), they got mainstreamed by their kids.

Now I must qualify this: I'm discussing what I've read about the Australian experience (I was far too young to experience it firsthand). First, they reject the term hippy in favour of "alternative lifestyler". According to them, they were different from American hippies, in that they had a plan for a permanent, low-impact alternative lifestyle - as opposed to simply dropping out. This involved living on the land, living off the land, with few modern conveniences.

But with free love came... children. They adjusted their lifestyle bit by bit. "What you want is not necessarily in the best interests of the children". The kids needed playgroups, schools, ... One couple switched away from vegetarianism because their daughter was "dead skinny and not thriving".


Undoubtedly others kept making a go of it. But by and large it seemed somewhat self-indulgent where children were suffering.

I'm not knocking their ideals at all. But it seems it was very hard to maintain an alternative lifestyle for the whole of the cycle of life.

Tech: identify the stars

SkyScout is an amazing device: it identifies stars.

It looks rather like a small video camera. Target it at any given star, and it will identify what it is. You can also locate a star or planet by selecting the name, then moving the device in the direction of the guiding arrows.

Astronomy - for me - is simply a confusing mass of bright spots in the sky. This is the sort of device that can help the astronomically challenged. Perhaps, for some, it may propel more people towards a more fundamental and fascinating subject: cosmology.

Climate change: costs and benefits of commuting options

For a company facing an impending move for hundreds of employees, a very interesting ready reckoner gave a comparison of commuting by public transport versus car:

Travel Time by car: 51 minutes
by public transport: 75 minutes

Weekly Cost for car: $194
for public transport: $33


Car costs took into account “fuel, insurance and servicing”, based on a mid-sized car, using NRMA data.

This reckoner was created to give a realistic understanding to employees of the commute to new premises next year. The user only had to enter a postcode to get the above table; the above is for mine (2031).

Rather a stark picture, isn’t it? For an extra 240 minutes per week, you’re paying $160. However, you’d also have to consider the amount of productive time you could gain in either situation – whether you wanted to read, snooze, or work, you can do it on public transport, but not in a car. So I’d really discount the time differential. The cost differential is approximately $7000 per year.

Everyone’s situation is different, but this is rather illustrative of the choice many people are making if they commute by car.